去る7月6日。「第一回 オフラインリアルタイムどう書く」が開催されました。
地理的時間的にわたしは参加できなかったのですが、お題が公開されたので解いてみました。
問題
三目並べ( tick-tack-toe )の手を入力とし、勝敗を出力する。
- 先攻がo、後攻がx
- すでに打ってある場所に打った場合、反則負け
- x が反則をした場合、「Foul : o won.」と出力
- 縦横斜めのいずれかで一列揃ったら、揃えた方の勝ち
- x が揃えた場合、「x won.」と出力
- 9マス埋まっても揃わなかったら引き分け
- 「Draw game.」と出力
- 勝敗が決した後の手は無視する
- 入力文字列は、先攻から順に打った位置を示す。盤上の位置と数の対応は下表を参照。
- 入力文字列が「91593」の場合、「oが9の位置、xが1の位置、oが5の位置、xが9の位置→xの反則負け(最後の3は無視)」となる。
- 以下の様なケースは考慮しなくてよい
- 入力が 1〜9 以外の文字を含んでいる
- 入力が不足していて、ゲームの勝敗が決まらない
2度目の解答。1度書いたあとになって、もう一段階いけるはず、という勘に従い半日ほど考えて出てきたのがこれです。ちょっとワキがあまいのはご愛嬌ということで。
#include <iostream> #include <string> enum Result { FAUL_X_WON, FAUL_O_WON, O_WON, X_WON, DRAW_GAME }; Result doukaku(const std::string& t) { unsigned int b[9] = { 0xb6b6u, 0xeeeeu, 0x5e5eu, 0xf5f5u, 0x2d2du, 0xddddu, 0x7373u, 0xebebu, 0x9b9b }; for(int i = 0; i < 9; ++i) { int n = t[i] - '0' - 1; int p = i % 2; if((b[n] ^ (b[n] >> 8)) & 0xffu) { return static_cast<Result>(p); } b[n] |= 0xffu << (8 * p); if(b[0] & b[1] & b[2] & b[3] & b[4] & b[5] & b[6] & b[7] & b[8]) { return static_cast<Result>(p + 2); } } return DRAW_GAME; } int main(int, char* []) { std::string s; while((std::cin >> s).good()) { switch(doukaku(s)) { case FAUL_X_WON: std::cout << "Faul: x won.\n"; break; case FAUL_O_WON: std::cout << "Faul: o won.\n"; break; case X_WON: std::cout << "x won.\n"; break; case O_WON: std::cout << "o won.\n"; break; default: std::cout << "Draw game.\n"; break; } } return 0; }
実行。
$ cat games.txt 79538246 35497162193 61978543 254961323121 6134278187 4319581 9625663381 7975662 2368799597 18652368566 965715 38745796 371929 758698769 42683953 618843927 36535224 882973 653675681 9729934662 972651483927 5439126787 142583697 42198637563 657391482 $ ./doukaku20120706 < games.txt x won. x won. x won. x won. x won. Faul: x won. Faul: x won. Faul: x won. Faul: x won. Faul: x won. o won. o won. o won. o won. o won. Faul: o won. Faul: o won. Faul: o won. Faul: o won. Faul: o won. Draw game. Draw game. Draw game. Draw game. Draw game.
ほとんどビット演算だけで解くことができました。
興味を持たれた方と、明日の自分のために、以下解説です。
勝負を判定する
ループ中の2つのif文で勝負の判定をしています。
1つ目で反則かどうか、2つ目でそろったかどうかを判定しています。
最初の手を第0手として0も偶数に含めると、偶数番目の手は「o」の手、奇数番目の手は「x」の手になります。
もしも偶数番目の手で反則があれば「o」の反則負け(「x」の勝ち)、奇数番目で反則があれば「x」の反則負け(「o」の勝ち)になります。
また偶数番目の手でそろったならば「o」の勝ち、奇数番目でそろったならば「x」の勝ちです。
9手目まで進んでも反則もそろってもないばあいは、盤がすべてうまっているはずなので引き分けになります。
まとめると。
| 0 | 偶数手 | 反則 | 「x」の勝ち |
| 1 | 奇数手 | 反則 | 「o」の勝ち |
| 2 | 偶数手 | そろった | 「o」の勝ち |
| 3 | 奇数手 | そろった | 「x」の勝ち |
偶奇は2の剰余で求まります。そろったばあいの勝敗は偶奇に+2することで求まります。
そろわず反則もなくループを抜けたら引き分けです。
これをもとに勝敗の値を決めました。
enum Result { FAUL_X_WON, FAUL_O_WON, O_WON, X_WON, DRAW_GAME };
そろったかどうかの判定
次にそろったかどうかの判定です。
最初に書いたコードではこの判定を次のように書いていました。
if( (board[0] & board[1] & board[2]) || (board[3] & board[4] & board[5]) || (board[6] & board[7] & board[8]) || (board[0] & board[3] & board[6]) || (board[1] & board[4] & board[7]) || (board[2] & board[5] & board[8]) || (board[0] & board[4] & board[8]) || (board[2] & board[4] & board[6]))
このコードではboard[ ]の値は「o」のときは1が「x」のときは2がはいります。まだ置かれていないばあいは0です。すると1列3マスの論理積をとると、3マスとも「o」か3マスとも「x」のばあいだけ非0となり、それ以外のばあいは0になります。最初のコードでは8とおりについて別々に判定していました。
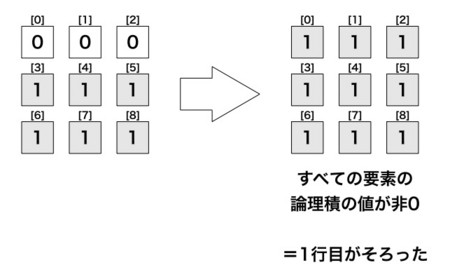
これを9マスすべての論理積で答えが出ないだろうか?と考えました。
結論から言うと。注目している列のマスのビットだけを最初は0にしておいて、他のマスのビットを1にしておきます。マスに手が打たれたらビットを書き込むようにすると、注目しているマスすべてに手が打たれれば全ビットの論理積が非0になります。
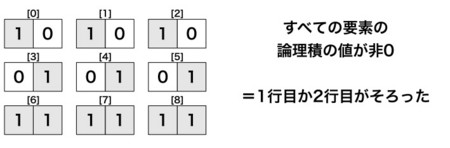
注目している列が2つだったばあいは2ビットで考えます。
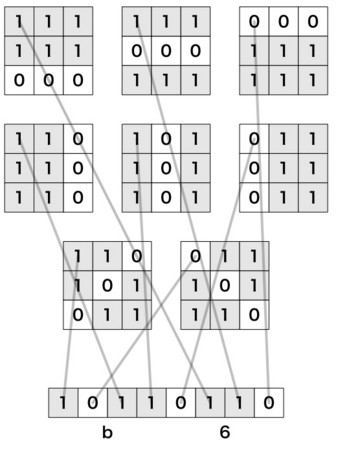
これらをすべてまとめると。縦横斜めで8とおりの並びがあるため、1マスあたり8ビットを割り当てればすべてのマスについて表すことができることがわかります。
また書き込む値は8つのビットがすべて1の、11111111(2)つまりFF(16)になります。これを「o」と「x」の2組持つ必要があるので計16ビットの値を各マスごとに与えることになりました。これが呪文のような初期値の正体です。
unsigned int b[9] = { 0xb6b6u, 0xeeeeu, 0x5e5eu, 0xf5f5u, 0x2d2du, 0xddddu, 0x7373u, 0xebebu, 0x9b9b };
偶数番目の手のときはビット0からビット7を、奇数番目の手のときはビット8からビット15を1で埋めています。
反則かどうかの判定
すでに手が打たれたマスかどうかの判定ですが、「o」用と「x」用のそれぞれに同じ値が繰り返していることを利用しています。そのままならば8ビットずつ同じ値が入っているので8ビットずらして排他的論理和を取れば下位8ビットは0になります。これがどちらかでも手が打たれていれば0にはなりません。
8ビットずらして下位8ビットが0か否かを見ることでそのマスがすでに埋まっているかどうかを判定することができるわけです。
if((b[n] ^ (b[n] >> 8)) & 0xffu)
「うまいやりかた」の功罪
今回のコードはそこそこ「うまくできた」という感触です。ただし、うまいプログラムがよいプログラムとは限らないのがプログラミングの妙です。それに「うまくできた」と思うものほど吸引力が強くて他の方法が思いつきづらくなるという弊害も。このコードを書いたあと別の言語のばあいも考えているのですが、考えがこのコードに引っ張られていて、その言語では不自然なやり方をしようとしていることに気付いたりします。
教訓――
わかりやすく書こう。――うますぎるプログラムはいけない。
いつか読むはずと読まない:たのしみ は たしなみ、たしなみ は たのしみ
ビット演算については「ハッカーのたのしみ―本物のプログラマはいかにして問題を解くか」で これでもか というぐらい解説がなされています。「ハッカーのたのしみ」という名にふさわしく、これがなんの役に立つのかと言いたくなるような技が並んでいます。ですが今回の解法のように以外とビット演算が活躍するケースがあります。三目並べを解くことが「活躍」するケースなのかはともかくとして。実用的な話ではバイトコードなどでビット演算で分岐を決めたりする設計などもあり、たしなんでおいても損はないかなと思っています。

ハッカーのたのしみ―本物のプログラマはいかにして問題を解くか
- 作者: ジュニア,ヘンリー・S.ウォーレン,Jr.,Henry S. Warren,滝沢徹,玉井浩,鈴木貢,赤池英夫,葛毅,藤波順久
- 出版社/メーカー: エスアイビーアクセス
- 発売日: 2004/09
- メディア: 単行本
- 購入: 35人 クリック: 732回
- この商品を含むブログ (128件) を見る
さかのぼって。
もともとビット演算を覚えたのはZ80のプログラミングをしているころでした。そのころよりどころとしていた本が「Z80 マシン語秘伝の書」です。これでプログラミングの基礎を学んだと言ってもいいぐらいです(ただし構造化プログラミング以前)。今回コードを書いているときも頭にちらちらと浮かんでくるのはこの本でした。Z80のプログラミングをする上でこれらの技はたしなみでしたが、これもまたたのしみのためだったりするわけです。

- 作者: 日高徹
- 出版社/メーカー: 啓学出版
- 発売日: 1989/08
- メディア: 単行本
- クリック: 4回
- この商品を含むブログ (1件) を見る
*1:新日本プログラミング