エンジニアのソフトウェア的愛情

または私は如何にして心配するのを止めてプログラムを・愛する・ようになったか

C++のtemplateが問題を解く

C++ Haskell ねた

そんなこんなで。@さんから「言語オタク」の称号を頂戴致しましたw。


そんな中で「C++のtemplate で問題を解く」という話をしたら、（ ゜д゜） な顔をされてしまいましたので、久々に「プログラミング言語 C++のtemplate」ねた。
C++マスターの面々はもっとすごいことをやっているので、マスターの方がここを見ていましたら「こいつ、またやってる」ぐらいに思って頂ければと。

道順を数える

残念ながら2年ぐらい前に事実上活動が停止してしまいましたが「どう書く？org」という互いにお題を出しては各種言語で実装を競い合う、コロシアムというか道場というかがありました。
そこにわたしが投稿したお題のひとつが「道順を数える」。

投稿した内容は次のようなものです。

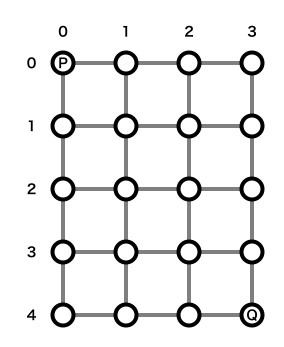
図.1のような。格子状の経路があるとします。

(1) このときPからQまでいくのに何通りの経路があるか数えてください。ただし遠回りはせずかならずQに近づく方向に進む(右方向か下方向にだけ進む)とします。

(2) (1)と条件は同じで、図.2のように経路の一部がない(通れない)場合に、PからQまでいくのに何通りの経路があるか数えてください。 

 P-+-+-+    P-+-+-+ 
 | | | |    | | | | 
 +-+-+-+    +-+-+-+ 
 | | | |    |   | | 
 +-+-+-+    +-+-+ + 
 | | | |    | | | | 
 +-+-+-+    +-+ +-+ 
 | | | |    | | | | 
 +-+-+-Q    +-+-+-Q 
   図.1       図.2

経路の表現の仕方、記憶の仕方は自由とします。上記のようなキャラクタでの表現でもよいですし、最初からプログラムで扱いやすいデータとして持っていてもOKです。入力も外部からの入力でもよいですし、プログラム中にコーディングされていてもOKです。


※問題は、野紾昭弘「離散数学『数え上げ理論』」(講談社 ブルーバックス)「第3章 道順を数える」から拝借させて頂きました。

グラフ理論の典型的な問題になると思いますが、グラフ理論はちゃんと学んでいないので、自分なりの言葉で解き方をまず解説します。


4行3桁のノードとそれぞれの間をつなぐエッジを考えます。

進める方向は、右方向、下方向のどちらかなので、あるノードへの経路は、上のノードからの経路のばあいと左のノードからの経路のばあいとがあります。このとき上のノードにたどり着くまでの経路の数がn、左のノードにたどり着くまでの経路がmであれば、当該ノードへの経路の数はn+mになります。
ただし、例外があって。左端のノードは左側にノードがないので上のノードからの経路だけになり、左端のノードの経路数は上のノードの経路数と同じになります。同様に上端のノードの経路数は左のノードの経路数と同じになります。また始点のノードの経路数は1（「始点から動かない」という1通りだけ）になります。


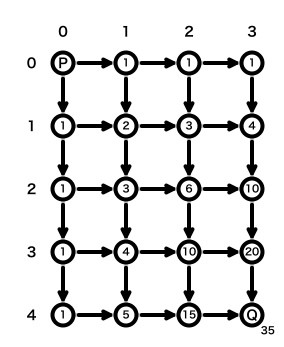
これらをすべて計算するして図にあらわすと次のようになり35通りという答えが得られます。

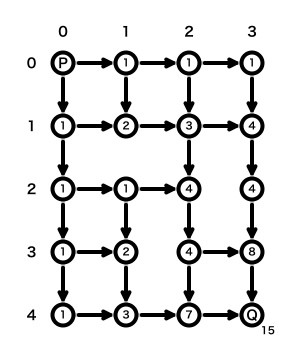
同様に図2のばあいは次のように15通りになります。

これらを、踏まえて。

まずはHaskellで解く

path 0   0   = 1                                       -- 始点（0行0桁の位置）のノードの経路数は1
path 0   col = path 0 (col - 1)                        -- 上端のノードの経路数はは左のノードの経路数と同じ
path row 0   = path (row - 1) 0                        -- 左端のノードの経路数はは上のノードの経路数と同じ
path row col = path row (col - 1) + path (row - 1) col -- それ以外のノードの経路数は左のノードの経路数と上のノードの経路数の和

main = print $ path 4 3 -- 終点（4行3桁の位置）のノードの経路数

path 0   0   = 1
path 2   1   = path 2 0 -- 2行1桁の位置のノードの経路数は左のノードの経路数と同じ
path 2   3   = path 1 3 -- 2行3桁の位置のノードの経路数は上のノードの経路数と同じ
path 3   2   = path 2 2 -- 3行2桁の位置のノードの経路数は上のノードの経路数と同じ
path 0   col = path 0 (col - 1)
path row 0   = path (row - 1) 0
path row col = path row (col - 1) + path (row - 1) col

main = print $ path 4 3


はい。なんのひねりもなく、解き方をそのままHaskellの文法で書き下すだけで答えを得ることができました。


これらを、踏まえて。

関数型プログラミング言語「C++のtemplate」で解く

これ以上解説の必要がないのでいきなりコードです。

// 各点での経路の数
template<char CHAR, template<int, int> class MAP, int ROW, int COL> struct C { static const int value = 0; };

// 経路を計算するテンプレート
template<template<int, int> class MAP, int ROW, int COL> struct Count { static const int value = C<MAP<ROW, COL>::value, MAP, ROW, COL>::value; };

// 各点での経路の数: キャラクタごとに特殊化
template<template<int, int> class MAP, int ROW, int COL> struct C<'s', MAP, ROW, COL> { static const int value = 1; };
template<template<int, int> class MAP, int ROW, int COL> struct C<'l', MAP, ROW, COL> { static const int value = Count<MAP, ROW, COL - 1>::value; };
template<template<int, int> class MAP, int ROW, int COL> struct C<'u', MAP, ROW, COL> { static const int value = Count<MAP, ROW - 1, COL>::value; };
template<template<int, int> class MAP, int ROW, int COL> struct C<'b', MAP, ROW, COL> { static const int value = Count<MAP, ROW - 1, COL>::value + Count<MAP, ROW, COL - 1>::value; };

// 問1の図を定義するテンプレート
template<int ROW, int COL> struct Map1         { static const char value = 'b'; }; // 基本的には左、上とも通れる
template<int COL>          struct Map1<0, COL> { static const char value = 'l'; }; // 0行目は基本的に左だけ通れる
template<int ROW>          struct Map1<ROW, 0> { static const char value = 'u'; }; // 0桁目は基本的に上だけ通れる
template<>                 struct Map1<0, 0>   { static const char value = 's'; }; // 0行0桁目は起点

// 問2の図を定義するテンプレート
template<int ROW, int COL> struct Map2         { static const char value = 'b'; }; // 基本的には左、上とも通れる
template<int COL>          struct Map2<0, COL> { static const char value = 'l'; }; // 0行目は基本的に左だけ通れる
template<int ROW>          struct Map2<ROW, 0> { static const char value = 'u'; }; // 0桁目は基本的に上だけ通れる
template<>                 struct Map2<0, 0>   { static const char value = 's'; }; // 0行0桁目は起点
template<>                 struct Map2<2, 1>   { static const char value = 'l'; }; // 2行1桁目は左だけ通れる
template<>                 struct Map2<2, 3>   { static const char value = 'u'; }; // 2行3桁目は上だけ通れる
template<>                 struct Map2<3, 2>   { static const char value = 'u'; }; // 3行2桁目は上だけ通れる

int anser1 = Count<Map1, 4, 3>::value; // 図1の4行3桁の位置のノードの経路数
int anser2 = Count<Map2, 4, 3>::value; // 図2の4行3桁の位置のノードの経路数


以上です。これで解けます。
おもむろにコンパイル。

$ g++ -S answer.cpp


このばあいanswer.sというファイルが生成されるのでその内容を見てみます（いつも通り、ターゲットのプロセサはPowerPC G4です）。

$ cat answer.s 
	.section __TEXT,__text,regular,pure_instructions
	.section __TEXT,__picsymbolstub1,symbol_stubs,pure_instructions,32
	.machine ppc7400
	.globl _anser2
	.data
	.align 2
_anser2:
	.long	15
	.globl _anser1
	.align 2
_anser1:
	.long	35
	.constructor
	.destructor
	.align 1
	.subsections_via_symbols


無事_anser1が35、_anser2が15と、正しい答えが得られました（爆）。



あとは@さんにPrologで解いてもらえれば万事OK


…


…ならいいな…。